Brain simulation 

Neural network is made from neurons and connections. The Framsticks simulator supports many types of neurons (for example sigmoid neuron N, noise generator Rnd, differential neuron D, delay neuron Delay, threshold neuron Thr), and users can easily create their own neurons (including sophisticated sensors and effectors) using FramScript and editing scripts/*.neuro files.

Formulas for neurons: N, Nu, D, Thr, *, Rnd, Sin, Fuzzy

Note: For most neurons, multiple inputs do not have individual meaning and are aggregated with respect to their weights (weighted sum is computed).

Neuron type How simulated
N and Nu
(sigmoid neurons)

In each simulation step:

#define NEURO_MAX 10.0
input=getWeightedInputSum();
velocity=force*(input-state)+inertia*velocity;
state+=velocity;
if (state>NEURO_MAX) state=NEURO_MAX;
else if (state<-NEURO_MAX) state=-NEURO_MAX;
tmp=state * sigmo;
N 
if (tmp<-30.0) output = -1;          //safer than exp(-tmp)
          else output = (2.0/(1.0+exp(-tmp))-1.0); // -1..1
Nu 
if (tmp<-30.0) output = 0;           //safer than exp(-tmp)
          else output = (1.0/(1.0+exp(-tmp)));     //  0..1

  • state, velocity – internal variables
  • sigmo, force, inertia – neuron parameters (properties)
  • input, tmp – temporary variables
D
(differentiate)		 Calculate the difference between the current and the previous input values.
Thr
(threshold)		 Outputs lo if the input signal is below the t threshold. Outputs hi otherwise.

t, lo and hi are parameters.
*
(constant output)		 Outputs the value of 1.
Rnd
(random noise)		 Outputs random values (uniform distribution) in the range of –1..+1
Sin
(sinus generator)

The output sinusoid has frequency f and initial phase t. The output frequency depends on the neuron input value. Parameters:

  • f0 (base frequency). The output frequency f = f0 + current_neuron_input_value.
  • t (time) – initial phase.
Fuzzy
(fuzzy control system)		 See this paper for details; see this video for demonstration.

The N neuron in detail

Sigmoid neurons (with short name N) use a simple weighted sum of input signals. Excitation influences neuron state, which has some inertia. Stronger signals can change the state faster than weak signals. Output is flattened to a [-1,+1] range using basic sigmoidal function. See examples below: (input/state/output)

Simple excitation. The state goes up when the input is positive and falls down when theinput reaches zero. Note that in this example the neuron's state can fall below zero due to its inertia.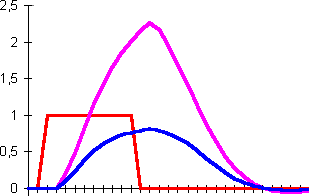
Short but strong impulse gives similar results to a weak and long one.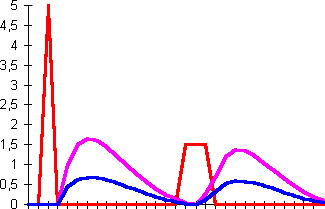
In this example a strong signal causes saturation of the neuron (its state goes very high). Later signal changes do not influence the output.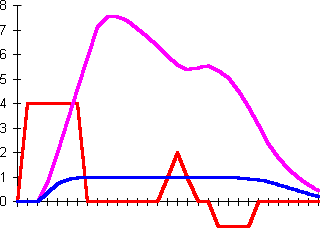

N parameters

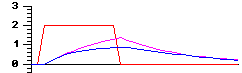
The 'N' neuron has three properties (parameters) which influence its behavior:
  • Force, noted as 'fo', value range: 0..1, default 0.04
  • Inertia, noted as 'in', value range: 0..1, default 0.8
  • Sigmoid, noted as 'si', any real number accepted, default 2.0
Force and inertia influence changes of the inner neuron state. In each simulation step, the neuron state is modified towards the value calculated from input excitations. Force determines how fast the value is changed. Maximum value of 1.0 gives instant reaction. Low values, like the default (0.04) cause smooth 'charging' and 'discharging' of the neuron. Neuron's inertia is similar to the physical inertia of a body: it sustains its state change tendency. Low inertia values have very little influence on the state. Values near the maximum (1.0) can result in oscillations of the neuron state. The following pictures show sample usage of these parameters (input/state/output).
Force=0.1, inertia=0
Slow state change. Note the instant reaction after the input signal pulse when inertia is disabled.
Force=0.1, inertia=0.8
With inertia enabled, the neuron's state rises above the input pulse amplitude, and then drops below zero. The final state is achieved after several oscillations.
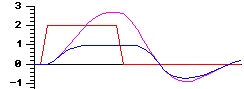Force=1, inertia=0
Maximum force coefficient results in an instant input to output propagation.

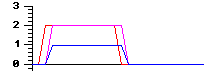The third, sigmoid coefficient changes the output function. Detailed formulas which describe the work of the N neuron are as follows:

    velocityt = velocityt–1 · inertia + force · (inputt – statet–1)

    statet = statet–1 + velocityt

    outputt =
    2  
    1 + e (-statet · sigmoid)
    		  – 1
    where
    input: weighted sum of neuron inputs,
    velocity: analogous to physical velocity,
    state: internal state (analogous to physical location),
    output: output signal.
    Subscripts represent the time moment.

    The following pictures show sample usage of the sigmoid parameter.

    Sigmoid=2.0
    Default.
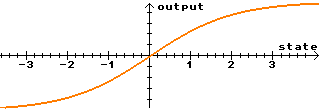    Sigmoid=10.0
    High values produce a threshold-like function.
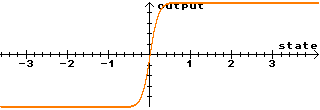    Sigmoid=0.5
    Low values give a nearly linear output function.
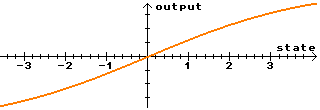